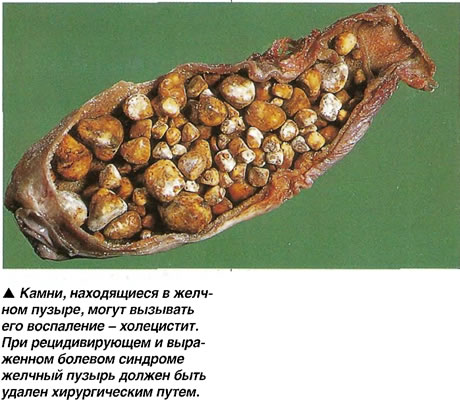
Что такое калькулезный: калькулезный - это... Что такое калькулезный?

Содержание

калькулезный — это… Что такое калькулезный?

калькулезный — (calculosus; лат. calculus камешек) относящийся к конкрементам, характеризующийся камнеобразованием … Большой медицинский словарь

гидронефроз калькулезный — (h. calculosa) Г., сочетающийся с наличием в почках конкрементов … Большой медицинский словарь

панкреатит калькулезный — (р. calculosa) П., обусловленный наличием в железе конкрементов или очагов обызвествления … Большой медицинский словарь

пиелонефрит калькулезный — (р. calculosa) П., сочетающийся с наличием конкрементов в почке или мочеточнике … Большой медицинский словарь

пионефроз калькулезный — (р. calculosa) П., обусловленный почечнокаменной болезнью … Большой медицинский словарь

холецистит калькулезный — (с. calculosa) X., при котором в желчном пузыре обнаруживаются конкременты … Большой медицинский словарь

Холецистит — I Холецистит (cholecystitis; греч.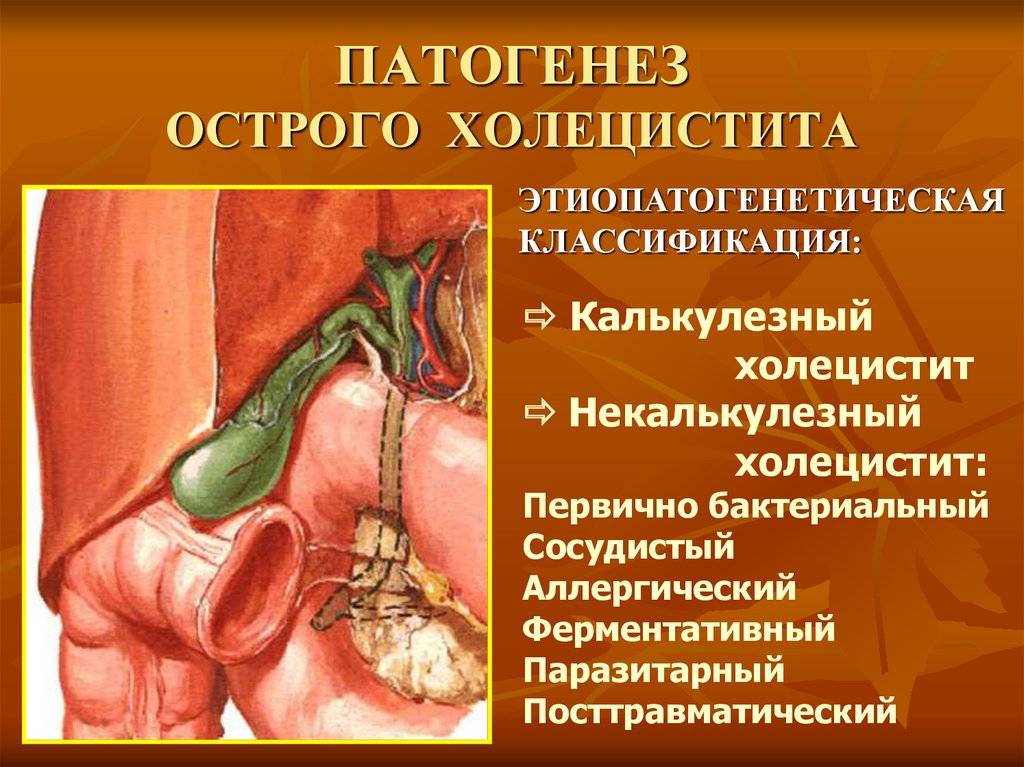 cholē + kystis пузырь + itis) воспаление желчного пузыря. Распространенное заболевание; встречается чаще у женщин, преимущественно среднего возраста. Причиной Х. является патогенная микрофлора, проникающая в… … Медицинская энциклопедия

пиелонефрит ксантогранулематозный — (р. xanthogranulomatosa) хронический калькулезный П., характеризующийся появлением в межуточной ткани почек микровключений гранулематозных пенистых и плазматических клеток … Большой медицинский словарь

Холецистит — (от греч. choly жёлчь и kýstis пузырь) воспаление жёлчного пузыря. Часто развивается при желчнокаменной болезни (См. Желчнокаменная болезнь) (т. н. каменный Х.), после гепатита вирусного (См. Гепатит вирусный) и др. инфекционных… … Большая советская энциклопедия

Желчнока́менная боле́знь — (cholelithiasis; синоним калькулезный холецистит) заболевание, обусловленное наличием конкрементов в желчном пузыре и желчных протоках.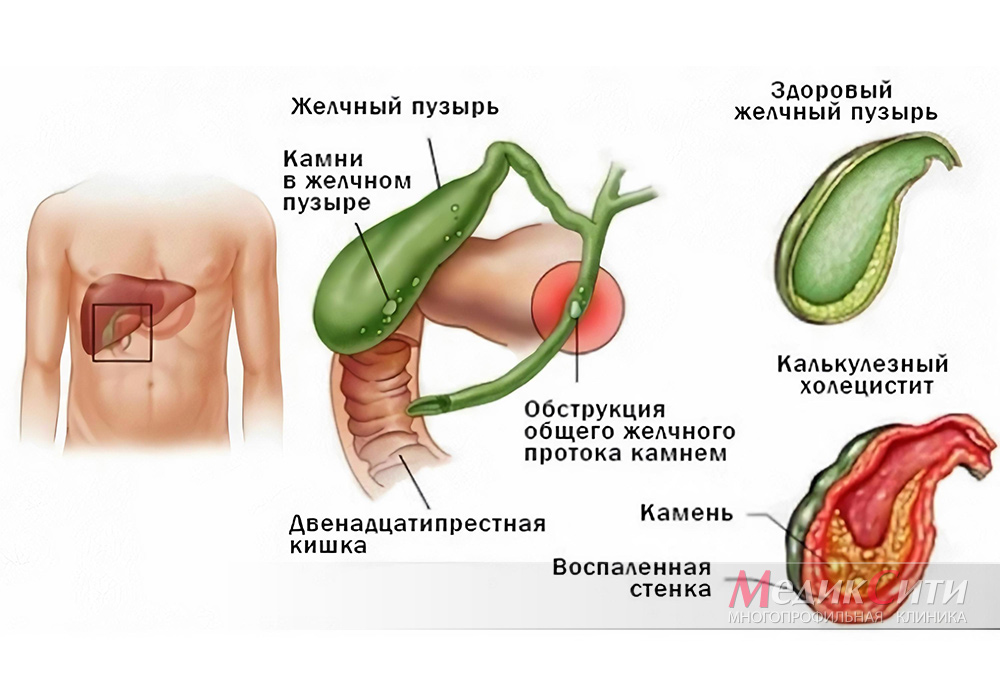 Частота образования желчных камней увеличивается с возрастом, достигая 45 50% у женщин старше 80 лет. У мужчин … Медицинская энциклопедия

Калькулезный холецистит — симптомы, лечение острого, хронического калькулезного холецистита

23 Мая 2018 г.

Калькулезный холецистит: хронический и острый

Неприятная на вид и горькая на вкус, желчь многими народами в прошлом воспринималась как причина дурного характера человека. Некоторая доля правды в этом действительно имеется: заболевания желчного пузыря вполне могут отравить жизнь человеку и всем окружающим заодно. Но в нормальных условиях желчь выполняет в организме целый ряд важных функций, большая часть которых связана с пищеварением.

Именно она создает в кишечнике среду, благоприятную для ферментов поджелудочной железы. С ее помощью из организма выводятся холестерин, билирубин и ряд других веществ, которые не фильтруются почками. Она активирует ферменты, необходимые для переваривания белков. Входящие в ее состав кислоты расщепляют жиры…

Желчь образуется в печени, часть ее накапливается в желчном пузыре. Когда человек есть, желчь из печени и желчного пузыря по протокам поступает в тонкую кишку. Но иногда с эвакуацией желчи возникают проблемы – она застаивается в желчном пузыре. В результате в этом органе развивается воспалительный процесс – холецистит.

Причины воспаления могут быть различны, но самая распространенная – наличие в желчном пузыре камней. Такую форму заболевания медики именуют калькулезным холециститом. Это один из видов желчнокаменной болезни.

Хронический калькулезный холецистит

Камни в желчном пузыре являются постоянным источником его воспаления. Но в хронической стадии этот процесс выражен слабо, болезнь лишь периодически дает о себе знать.

Проявления хронического калькулезного холецистита:часто возникающая ноющая боль в правом подреберье;

приступообразные боли, возникающие после употребления жирной, соленой или жареной пищи;
тошнота и отрыжка с горьким привкусом;
отдельные приступы рвоты с желчью.

Впрочем, на этой стадии заболевания симптомы могут быть настолько слабо выражены, что не воспринимаются как признаки тяжелой патологии. Пациент может регулярно испытывать «всего лишь» чувство тяжести в правом боку, страдать от метеоризма, поносов, изжоги, отрыжки, ощущать горечь во рту…

Временами хронический калькулезный холецистит проявляется приступами печеночной колики. При этом наблюдается сильная колющая боль в правом подреберье, которая иногда сопровождается рвотой. В момент приступа язык становится сухим, живот напряжен. При этом анализ крови не выявляет нарушений, а желчный пузырь и печень не увеличены.

Приступ колики может продолжаться от нескольких минут до нескольких часов.

Острый калькулезный холецистит

Причиной острой формы калькулезного холецистита становятся камни, обтурирующие (закупоривающие) шейку желчного пузыря. При этом прекращается отток желчи, а в самом пузыре развивается инфекция.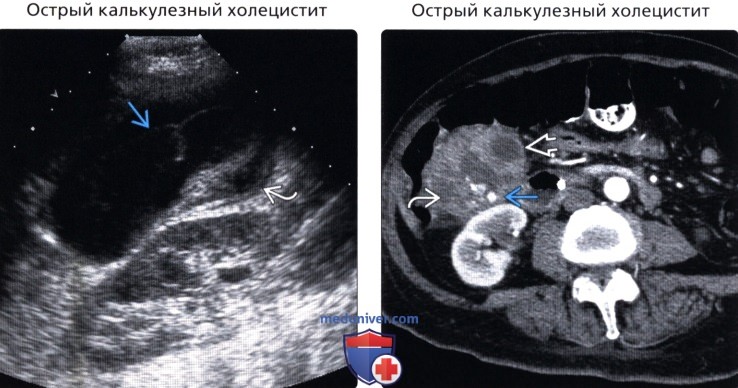 Проявляется заболевание резкой болью в правом подреберье, тошнотой, многократной рвотой, слабостью.

Приступ острого калькулезного холецистита имеет некоторые различия с «обычной» печеночной колики. Прежде всего, это повышение температуры, признаки воспаления в анализе крови – нейтрофильный лейкоцитоз, увеличенная скорость оседания эритроцитов, изменения на УЗИ.

Если не удается добиться эффекта от консервативной терапии в первые сутки-двое, пациента приходится оперировать. Экстренная операция более сложная и имеет больший риск развития осложнений.

Лечение острого калькулезного холецистита

В первые часы после начала приступа острого калькулезного холецистита проводятся консервативные мероприятия:

голодание;
холод на живот;
обезболивание;
внутривенное введение спазмолитических препаратов, антибиотиков;
дезинтоксикационная терапия для нормализации функции печени и почек.

Все эти действия способны снять симптомы обострения, но ни в коем случае не помогают ликвидировать причину – само заболевание. Единственный надежный метод лечения калькулезного холецистита, как и желчнокаменной болезни в целом – хирургическое удаление желчного пузыря.

Автор
Ларин Сергей Вячеславович , Хирург, онколог

Причины калькулезного простатита и методы лечения

Калькулезный простатит является хронической формой воспалительного процесса, которая протекает в области простаты. Заболевание сопровождается образованием конкрементов выводных протоков железы.

Простатит поражает с каждым годом все большее число мужчин. Связано это со склонностью к ведению малоподвижного образа жизни, неразборчивыми половыми связями, мутированием вирусов со снижением их чувствительности к антибактериальным средствам. Хронический калькулезный простатит является наиболее распространенной формой заболевания.

Острое воспаление часто осложняется образованием камней и может приводить к аденоме предстательной железы и раннему угасанию половой функции.

Хронический калькулезный простатит

Хронический простатит — калькулезная форма может быть как в вторичной, так и первичной. Первично камни образуются в протоках железы, вторично — поступают в простату из почек, уретры и мочевого пузыря. Заболевание нередко развивается при наличии мочекаменной болезни.

Основные предрасполагающие факторы:

доброкачественная гиперплазия предстательной железы;
малоподвижный образ жизни;
мочеполовые инфекции, которые приводят к обструкции протоков простаты и сгущению ее секрета;
застойные процессы в органах малого таза;
уретро-простатический рефлюкс, который сопровождается забросом незначительного количество мочи при мочеиспускании из области уретры в протоки простаты.

Основной причиной развития хронического калькулезного простатита является стриктура уретры. На ее фоне происходит заброс мочи в протоки предстательной железы. Происходящая в дальнейшем кристаллизация приводит к формированию камней.

Клинические проявления заболевания наиболее заметны при обострении хронического воспалительного процесса. Ведущим симптомом является болевой синдром. Боли при калькулезном простатите тупые и ноющие, локализуются преимущественно в области лобка и промежности, могут появляться в пояснице. Усиление болевого синдрома нередко связано с интимными контактами, повышенными физическими нагрузками, мочеиспусканием и дефекацией. Также боль вызывает продолжительное ходьба.

Нередко конкременты предстательной железы специалисты обнаруживают совершенно случайно во время комплексного обследования. Но при тяжелом течении заболевание может приводить к острой задержке мочи, абсцессу, гематурии, снижению полового влечения и импотенции.

Хронический калькулезный простатит лечение

При правильном лечении риск обострения простатита минимален. Остерегайтесь заражения венерическими инфекциями, не переохлаждайтесь, избегайте повышенных физических нагрузок и стрессов. Для надежной профилактики рекомендуется после угасания острой воспалительной реакции принимать специальные пробиотики, способные увеличивать количество полезных микроорганизмов, обитающих на слизистой мочеиспускательного канала. Это повысит устойчивость к патогенам и сведет на нет риск обострения простатита.

Стоимость услуг по лечению калькулезной формы простатита

Стоимость лечения калькулезного простатита зависит от выраженности клинических проявлений, длительности течения заболевания и многих других факторов. Цена включает проведение обследования, которое позволяет правильно поставить диагноз и подобрать лечебные методики.

В нашей клинике лечением хронического калькулезного простатита занимаются квалифицированные урологи, в распоряжении которых имеются все необходимые диагностические и лечебные методики.

Так же смотрите по теме:

что это такое, причины, признаки, симптомы, лечение – МЕДСИ

Холецистит представляет собой воспалительный процесс в желчном пузыре, который может привести к такому осложнению, как желчнокаменная болезнь. Оно дает о себе знать сильной болью и дискомфортом в правом боку.

По статистике, его распространенность достигает 20%, а наиболее подвержены его появлению женщины старше 50-ти лет.

Классификация

Для классификации холецистита применяется несколько подходов:

Хронический холецистит проявляется постепенно, сопровождается эпизодическим появлением дискомфорта в правом боку (включая хронический калькулезный холецистит).

По характеру новообразований:

Без появления конкрементов (камней) в желчном пузыре (более вероятен для пациентов младше 30-ти лет)
С формированием камней в пузыре

По типу проявления:

Хронический
Острый – может проявиться при формировании камней на фоне развития желчнокаменной болезни

По степени воспаления:

Гнойный
Катаральный – сопровождается сильными болями с правой стороны, которые могут также ощущаться в пояснице, правой части шеи, правой лопатке
Флегмонозный – сопровождается болями при кашле, перемене положения тела в пространстве и др.
Гангренозный – в него перерастает холецистит на флегмонозной стадии
Смешанный

Причины

Причины возникновения:

Болезни ЛОР-органов и дыхательных путей (гайморит, бронхит, синусит, пневмония и др.)
Появление хронических или острых воспалительных процессов в желудочно-кишечном тракте (дисбактериоз, колит, аппендицит и др.)
Возникновение паразитов протоках желчного пузыря (лямблиоз и т. п.)
Развитие инфекций половой или мочевыводящей систем (цистит, пиелонефрит, оофорит, простатит и др.)

Одним из факторов риска является чрезмерное употребление острых, жирных или жареных продуктов.

Факторы риска:

Наличие дискинезии желчевыводящих путей (нарушение тонуса мышц, может спровоцировать проблемы с оттоком желчи)
Неправильный состав желчи (возникает из-за неправильного питания)
Попадание содержимого двенадцатиперстной кишки в желчные ходы и в желчный пузырь
Аутоиммунные процессы
Патологии развития желчного пузыря
Нарушение кровоснабжения органа (из-за артериальной гипертензии или сахарного диабета)
Изменение гормонального фона по причине нарушения менструального цикла, беременности и др.
Ожирение
Чрезмерное употребление острых, жирных или жареных продуктов
Злоупотребление алкогольсодержащими напитками и табачными изделиями
Генетическая предрасположенность
Аллергические реакции

Холецистит у взрослых — симптомы

Первым признаком заболевания является появление болей с правой стороны (под ребрами). Данный симптом может купироваться обезболивающими препаратами, но затем дискомфорт в этой области будет возвращаться снова.

Первым признаком заболевания является появление болей с правой стороны (под ребрами).

Холецистит – признаки заболевания:

Нарушение пищеварения
Присутствие болевых ощущений справа (может проецироваться в область правой руки или лопатки)
Постоянная тошнота, отрыжка
Озноб
Пожелтение кожных покровов
Нарушение аппетита
Чрезмерное газообразование

Подобные симптомы могут проявляться как одновременно, так и по отдельности. Признаки острой и хронической форм заболевания могут различаться.

Хронический холецистит – симптомы:

Тяжесть и боль в правом боку, под ребрами, в лопатке
Регулярная отрыжка и горечь во рту
Постоянные проблемы с пищеварением (отсутствие аппетита, тошнота и рвота и др.)
Проявление желтушных признаков

При остром приступе холецистита появятся такие симптомы:

Внезапная слабость и горечь во рту
Человеку не удобно любое положение, при этом участился пульс и понизилось давление
Сразу после приема пищи происходит рвота
Кожные покровы пожелтели
Справа появилась острая боль

Как снять приступ холецистита?

При появлении холецистита и его острых признаков необходимо лечение. Поэтому первым делом необходимо вызвать врача скорой помощи.

Во время ожидания приезда доктора следует:

Обеспечить состояние покоя для больного
Дать обезболивающее (спазмолитик)
Наложить холодный компресс

Во время ожидания приезда доктора следует поить пациента минеральной водой без газа (хлоридно-натриевой), особенно после рвоты.

Что нельзя использовать при приступе холецистита и его симптомах перед лечением:

Прикладывать грелку
Применять наркотические обезболивающие или анальгетики
Принимать алкогольные напитки
Делать клизму
Использовать какие-либо лекарства кроме спазмолитиков

Осложнения

Если любое заболевание не лечить своевременно, его развитие может привести к тяжелым последствиям. В случае с холециститом возможно появление таких осложнений, как:

Прекращение работы желчного пузыря
Реактивный гепатит
Появление свища в органах желудочно-кишечного тракта
Развитие холангита – воспаления желчных протоков
Появление эмпиемы желчного пузыря – сопровождается воспалением и скоплением гноя
Возникновение гангрены и перитонита
Разрыв желчного пузыря
Перихоледохеальный лимфаденит – воспаление лимфоузлов
Непроходимость кишечника

Появления всех осложнений можно избежать, если вовремя обратиться к врачу.

Диагностика

При постановке диагноза врач-гастроэнтеролог опрашивает пациента, собирает анамнез и осматривает.

Для более точной постановки диагноза необходимо провести ряд лабораторных исследований.

Лабораторные исследования:

Общий анализ мочи
Анализы крови:

На сахар, холестерин и панкреатическую амилазу (для выявления сопутствующих заболеваний)
Общий (для выявления признаков воспаления)
На антитела к паразитам (для выявления лямблий)
Биохимический (для определения повышения активности трансаминаз АСТ, АЛТ, ГГТП, щелочной фосфатазы и билирубина, появляющихся при хроническом холецистите)

Анализы кала:

На антитела к паразитам (выявление лямблий)
Копрограмма

Для уточнения диагноза или выявления сопутствующих патологий врач может назначить ряд таких процедур, как:

ЭКГ
УЗИ брюшной полости
КТ или МРТ с контрастом
УЗИ с желчегонным завтраком (для выявления дискинезии)
Билиосцинтиграфия (радиоизотопное исследование)
ЭРПХГ (эндоскопическая ретроградная панкреатохолангиография)
Посев желчи
Рентгенография органов брюшной полости
Дуоденальное зондирование
Эндоскопическое ультразвуковое исследование (эндоУЗИ)

Холецистит – лечение у взрослых

Как и другие заболевания, холецистит требует своевременного лечения. Общие принципы терапии холецистита:

Применение антибиотиков
Назначение диеты
Лечение симптомов
Применение физиотерапии

При хроническом холецистите лечение может быть как медикаментозным, так и хирургическим.

Для комплексной лекарственной терапии применяются следующие типы препаратов:

Антибиотики
Ферменты для облегчения пищеварения
Спазмолитики
Противовоспалительные средства (нестероидные)
Прокинетики (для обеспечения корректной работы ЖКТ)
Средства, содержащие бифидо-и лактобактерии
Желчегонные препараты

Также рекомендуется применять физиотерапевтические процедуры и пройти санаторно-курортное лечение.

При холецистите лечение обострения может быть хирургическим в случае невозможности снятия острого воспаления медикаментами. В такой ситуации пораженная часть желчного пузыря удаляется.

Диета

Можно есть такие блюда и продукты, как:

При холецистите важной частью лечения является питание.

Овощные и молочные супы
Блюда, приготовленные на пару или в духовке (мясо, нежирная рыба)
Нежирные молочные продукты
Яйца в виде белковых омлетов
Не кислые фрукты и овощи
Крупы и макароны
Не кислое варенье
Несладкое печенье, хлеб, сухари
Зелень (петрушка, укроп)
Корица, ваниль
Неострые соусы (включая соевый)
Мармелад, сухофрукты, конфеты без содержания какао и шоколада

При холецистите во время лечения диета должна исключать:

Жареное, острое, соленое, кислое, жирное
Острые приправы (майонез, аджика, кетчуп и др.)
Жирные молочные продукты
Бобовые, грибы
Яйца с желтками
Кофе, алкоголь, какао, газированные напитки
Шоколадосодержащие продукты (выпечка, конфеты)
Кислые или острые овощи и зелень

Преимущества проведения процедуры в МЕДСИ

Клиники МЕДСИ располагают современным экспертным оборудованием для проведения точной и быстрой диагностики
При диагнозе «холецистит», его симптомах и лечении у взрослых специалисты МЕДСИ используют только инновационные методики лечения
Пациентам предлагаются комфортные условия пребывания в стационаре
В клиниках отсутствуют очереди и необходимость длительного ожидания
При постановке сложного диагноза может быть собран врачебный консилиум
Существует возможность оперативной записи на прием по телефону 8 (495) 7-800-500

Клиники МЕДСИ располагают современным экспертным оборудованием для проведения точной и быстрой диагностики

«Что такое калькулезный холецистит?» – Яндекс.Кью

Калькулезный холецистит — это наличие в желчном пузыре (по результатам дополнительного обследования — УЗИ, МРТ или КТ) камней и, как следствие изменение в самом органе.

Для определения правильной тактики лечения камней в желчном пузыре необходимо уточнить из чего они предположительно состоят: холестериновые камни (при УЗИ не «отбрасывают» эхо-негативную тень) или камни из желчных кислот (имеют такую тень при проведении УЗИ).

Холестериновые камни могут «рассасываться», для этого могут применяться препараты, для их частичного «растворения», например Урсосан или его аналоги.
Камни, состоящие из желчных кислот, как правило, не «рассасываются». Для их удаления во избежание развития приступа «желчной колики» или «острого холецистита» в плановом порядке рекомендуется проведение операции по удалению желчного пузыря. Эти острые состояния могут развиваться и при наличии мелких камней (если камень «закроет» просвет желчного протока) и опасны в первую очередь своими осложнениями (присоединение инфекции, поражение печени и поджелудочной железы) и характеризуются выраженным болевым синдромом (при развитии операция проводится в экстренном порядке).

На сегодняшний день большинство таких операция проводится лапароскопическим методом (если нет для этого противопоказаний), то есть с минимальным вмешательством в брюшную полость.Важно отметить, что для выбора правильно тактики лечения важную роль играет не только размер, но и их количество. Решение о схеме лечения должен принимать врач-хирург по результатам осмотра и обследования.Стоит помнить, что после удаления желчного пузыря необходимо соблюдать диету — ограничивать жиры в продуктах питания (исключить сливочное масло, майонез, «жирную» сметану, творог и сыры, колбасные изделия и «жирные сорта» мяса, продукты лучше употреблять в отварном или запеченном виде), ограничивать прием алкоголя.

Хронический калькулезный холецистит

Однопортовая лапароскопическая холецистэктомия SILS

Однопортовая лапароскопическая холецистэктомия SILS
Оперирует профессор К. В. Пучков (2020 г).

У пациентки большой желчный пузырь, который уже практически не функционирует.

Пучков К. В. выполняет ей холецистэктомию по методике SILS через один порт. Суть метода сводится к выполнению лапароскопической холецистэктомии через специальный порт (устройство), который вводится в пупочную область и вы его наглядно увидите. Диаметр порта составляет 23-24 мм. Через него проводят лапароскопические инструменты и лапароскоп диаметром 5 мм.

После окончания операции устройство вместе с желчным пузырем извлекается из брюшной полости. На маленькую рану в пупочной области накладывается косметический шов.

Подробнее о методике Вы можете прочитать на личном сайте профессора Пучкова Константина Викторовича перейти

Однопортовая холецистэктомия по методике SILS. Операция при ЖКБ

Однопортовая холецистэктомия по методике SILS. Операция при ЖКБ
Оперирует профессор К. В. Пучков (2020 г).

В видео представлена трансляция, где Пучков К.В. выполняет операцию по поводу желчнокаменной болезни — холецистэктомию через единый порт (методика S.I.L.S.), всего через один прокол.

Симультанная лапароскопическая гистерэктомия и холецистэктомия через единый лапароскопический доступ (S.I.L.S. Port, COVIDIEN)

Симультанная ларароскопическая гистерэктомия и холецистэктомия через единый лапароскопический доступ (S.I.L.S. Port, COVIDIEN).
Оперирует профессор К. В. Пучков (2019 г).

В фильме показана техника лапароскопической холецистэктомии через единый порт (SILS порт COVIDIEN) при хроническом калькулезном холецистите. Размер жёлчного пузыря 12х4 см. Показана техника транскутанных фиксирующих швов, выделение пузырного протока и артерии инструментом mini retract COVIDIEN и клипирование этих структур автоматическим 5 мм апликатором. Гистерэктомия проводится с помощью 10 мм инструмента LigaSure MEDTRONIC COVIDIEN. На первом этапе пересекаются круглые связки. Затем последовательно воронко-тазовые и крестцово-маточные. Далее монополярным электродом рассекается пузырно-маточная складка и отсепаровывается задняя стенка мочевого пузыря от передней стенки влагалища. Далее проводится кольпотомия, с последующим извлечением матки и желчного пузыря в контейнере вагинальным путем. Ушивание стенок влагалища и крестцово- маточных связок, а также перитонизация брюшины проводится с помощью инструмента Endo Stitch COVIDIEN, нитью Полисорб 2-0 узловыми швами.

Симультанная лапароскопическая кардиомиотомия с парциальной фундопликацией в модификации Волковой и холецистэктомия

Симультанная лапароскопическая кардиомиотомия с парциальной фундопликацией в модификации Волковой и холецистэктомия
Оперирует профессор К. В. Пучков (2018 г).

Операция проводится при ахалазии кардии 3 стадии хроническом калькулезном холецистите. В фильме показана техника диссекции пищеводно- желудочного перехода 5 мм инструментом LigaSure MEDTRONIC COVIDIEN. Кардиомиотомия выполнена по оригинальной методике тонким монополярный электродом в режиме пониженной мощности. Обращается внимание на пересечение всех мышечных слоёв до подслизистого слоя на расстоянии не менее 8 см. Затем дефект укрывается передней стенкой желудка с фиксацией непрерывным интракорпоральным швом. В конце этого этапа проводится передняя крурорафия, рассеченных ножек диафрагмы. Далее показана техника лапароскопической холецистэктомии при хроническом калькулезном холецистите. Особое внимание на этом этапе уделяется тщательной диссекции трубчатых структур в зоне треугольника Кало. После диссекции пузырного протока и артерии, а также визуализации латеральной стенки холедоха, выделенные структуры пересекаются между клипсами. 10 мм аппликатор вводится из рабочего доступа в левом подреберье. Удаленный желчный пузырь извлекается из брюшной полости в пластиковом контейнере.

Подробнее о методиках Вы можете прочитать на личном сайте профессора Пучкова Константина Викторовича перейти

Лапароскопическая холецистэктомия, диссекция треугольника Кало

Лапароскопическая холецистэктомия, диссекция треугольника Кало.
Оперирует профессор К. В. Пучков (2018 г).

В фильме показана техника лапароскопической классической холецистэктомии при хроническом калькулезном холецистите. Особое внимание на этом этапе уделяется тщательной диссекции трубчатых структур в зоне треугольника Кало монополярным электродом (этот этап специально показан без монтажа). После диссекции пузырного протока и артерии, а также визуализации латеральной стенки холедоха, выделенные структуры пересекаются между клипсами. 10 мм аппликатор вводится из рабочего доступа в левом подреберье (он использовался для выполнения кардиомиотомии по поводу ахалазии кардии). Удаленный желчный пузырь извлекается из брюшной полости в пластиковом контейнере.

Лапароскопическая холецистэктомия при выраженном спаечном процессе (конкремент 5,5 см, объём содержимого 400 мл)

Лапароскопическая холецистэктомия при выраженном спаечном процессе (конкремент 5,5 см, объём содержимого 400 мл).
Оперирует профессор К. В. Пучков (2018 г).

В фильме показана техника лапароскопической холецистэктомии при хроническом калькулезном холецистите и выраженном спаечном процессе. Размер жёлчного пузыря 22×4 см (объем 300 мл), размеры камня 5,5 см. Показана техника выделения желчного пузыря из спаек с помощью 5 мм инструмента (LigaSure MEDTRONIC COVIDIEN) и монополярного электрода. Свободным от спаечного процесса было только дно желчного пузыря. Далее выполнялось тщательное выделение пузырного протока и артерии 5 мм монополярным крючком и инструментом mini retract COVIDIEN и клипирование этих структур 10 мм аппликатором Aesculap DS титановыми клипсами с защелкой. Удаленный желчный пузырь извлекается из брюшной полости в пластиковом контейнере.

Лапароскопическая холецистэктомия через единый доступ (S.I.L.S. Port COVIDIEN)

Лапароскопическая холецистэктомия через единый доступ (S.I.L.S. Port COVIDIEN).
Оперирует профессор К. В. Пучков (2018 г).

В видео операции показана техника лапароскопической холецистэктомии через единый порт (SILS порт COVIDIEN) при хроническом калькулезном холецистите. Размер жёлчного пузыря 14×7 см. Даются комментарии по установке порта. Учитывая большие размеры желчного пузыря, проводится его пункция и эвакуация 100 мл густой желчи. Показана техника транскутанных фиксирующих швов, тщательное выделение пузырного протока и артерии 5 мм монополярным крючком и инструментом mini retract COVIDIEN и клипирование этих структур автоматическим 5 мм аппликатором. Удаленный желчный пузырь извлекается из брюшной полости в пластиковом контейнере.

Подробнее о методиках Вы можете прочитать на личном сайте профессора Пучкова Константина Викторовича перейти

Хронический калькулезный холецистит. Лечение от _ руб. в Клинике ABC. Обострение хронического калькулезного холецистита лечение

Хронический калькулезный холецистит ― это осложненное течение желчекаменной болезни с воспалением пузырной стенки. Ткани гипертрофируются, отекают, как следствие нарушается эвакуаторно-моторная функция. То есть патология не обособленная, а часто сопровождается дискинезией. Если не проводится лечение, нарастает атония. Такое состояние еще называют «мертвый желчный пузырь».

Останавливается он из-за облитерации камнями. Лечение хронического калькулезного холецистита включает нормализацию состава желчи, устранение инфекции, опорожнение и дренирование. Народная медицина не способна справиться с заболеванием. Рекомендуется гастроэнтерологами как вспомогательное средство.

Конкременты находятся в теле или протоках пузыря, бывает смешанная локализация. Одиночные камни не менее опасны, чем множественные. Они так же подвижны, перекрывают холедох. При сокращениях и выбросе желчи царапают слизистую. Когда орган опорожнен, ущемляются между складками, оказываемое ими давление приводит к пролежням.

Увеличивается число случаев холецистита у детей. Мужская и женская тенденция меняется с возрастом. Мальчики до 6-8 лет болеют в 2-3 раза чаще девочек, после 12 лет наоборот. Ведущей причиной является нарушение режима питания, замена домашней еды продуктами быстрого приготовления (пельмени, заварная вермишель), злоупотребление сладостями с красителями, чипсами. Прием пищи должен быть дробный, с меню из натуральных продуктов, минимальным количеством специй, жиров.

Бессимптомная стадия приходится на момент образования сладжей, вялотекущего воспаления. Калькулезная форма происходит из безкалькулезной или ЖКБ. Поэтому человеку трудно заметить изменения в организме. При любом дискомфорте в эпигастрии или кишечнике, чувстве тяжести после еды, подташнивание, нужно обратиться к врачу.

Анатомическая и генетическая предрасположенность

30% холецистита связаны с аномальным строением желчного пузыря, без погрешностей в режиме питания. Неправильное формирование органа во время внутриутробного развития становится причиной застоя секреторной жидкости и ее слабого выброса. При аплазии орган недоразвит, желчь поступает непосредственно из печеночного протока в холедох. Гипоплазия характеризуется быстрым выбросом, ввиду того, что полость меньше нормы.

В первом случае, страдает холедох, сосочек 12-перстной кишки. Во втором, возникает холецистит, так как кислоты не успеваю разжижать желчь, из-за высокой вязкости на стенках оседают билирубиновые, холестериновые сладжи.

Также ухудшает перистальтику неправильная форма, локализация:

слева, поперек, внутри печени
слабая фиксация (есть риск перегиба)
две доли, много камер, удвоение, трипликация
шаровидная, S-образная форма и бумеранг

40-55% холецистита составляет зависимость от наследственных факторов, без отклонений в анатомии. Родовая динамика может быть в виде шахматной доски или идти из поколения в поколение. В большей степени это только предрасположенность, а значит его можно избежать с помощью профилактики, своевременного лечения ЖКТ.

Лечение обострения хронического калькулезного холецистита бывает медикаментозное и хирургическое. Если есть перитонеальные осложнения или желчный не выполняет свою функцию, его удаляют. При сохранении целостности, моторики, свободном протоке, единичных камнях, лечение консервативное.

Профилактика и ключевые симптомы

Профилактика холецистита направлена на нормализацию обмена веществ, моторной и секреторной функции. Поэтому способствует стабилизации всей системы пищеварения. Разделяйте прием пищи на 5-6 раз дробными порциями. Исключите жирные, острые, жареные продукты. Употребляйте 1,5-2 литра жидкости в день.

Пройдите диспансерное обследование, чтобы выявить сопутствующие заболевания:

гастрит
язва желудка
цирроз печени
вирусный гепатит
сахарный диабет
панкреатит

Лечение ЖКТ и правильное питание уменьшают влияние провоцирующих факторов. К группе риска относятся люди с ожирением, беременные, женщины старше 50 лет.

Даже если проявления неспецифические, нужно обратиться к гастроэнтерологу. Расстройство стула, тошнота, отрыжка ― общие признаки. На область поражения указывает место боли ― правое подреберье. К специфическим симптомам относится:

Желтушность склер, кожи, слизистых.
Зуд кожи.
Моча цвета пива.
Белый кал.
Печеночная колика.

Острый хронический калькулезный холецистит сопровождается болезненным спазмом, отдающим в правое плечо, под лопатку, шею. Желтуха, зуд становятся выраженными, так как нарастает интоксикация. Присоединяется головная боль, замедление пульса, падение АД. Тошнота переходит в непрерывную рвоту горечью.

Нельзя ставить грелку на правое подреберье, тепло поспособствует воспалению. Вызовите скорую помощь, примите спазмолитики, но не другие обезболивающие, они смажут клиническую картину, но не уберут спазм. Не медлите с экстренным лечением. Острые камни травмируют стенки, протоки органа вплоть до разрыва. Закупорка холедоха провоцирует водянку, эмпиему.

Запишитесь на прием по телефону
+7 (495) 021-12-26 или заполнив форму online

Администратор свяжется с Вами для подтверждения записи.
Конфиденциальность Вашего обращения гарантирована.

Как лечить холецистит с ЖКБ?

Хронический калькулезный холецистит в стадии обострения лечится противовоспалительными, спазмолитическими препаратами. Для расслабления мышечных волокон назначается пероральное (таблетки) или парентеральное (инъекции) введение Папаверина, Но-шпы, Баралгина, Атропина. По показаниям лечение дополняется новокаиновой блокадой.

Для компенсации гепатобилиарной системы, устранения инфекции выписываются:

Гепатопротекторы: Гептрал, Гепабене, Эссенциале, Фосфоглив.
Ферменты: Панзинорм, Креон, Фестал, Мезим.
Антибиотики: Цефоперазон, Амоксициллин, Тобрамицин, Цефепим, Метронидазол.

Первые три дня нужен покой и голод. Пациент соблюдает постельный режим. Нельзя есть, только пить некрепкий чай, сок, отвар шиповника. Литолитики для разрушения конкрементов противопоказанны в острой фазе.

Решение о холецистэктомии принимается в первые трое суток. Операция показана при перитоните, пристеночном инфильтрате, напряженной водянке.

Если нет экстренных показаний, пациент продолжает консервативное лечение. С 4-го дня переходит на диету №5В. Рацион дополняется слизистыми супами, протертыми кашами, сухарями, киселем. С 9-10 дня лечебный стол №5А. Меню дополняется супом-пюре, паровым омлетом, 1% кефиром, суфле из нежирного мяса, картофельным и морковным пюре.

Хронический калькулезный холецистит желчного пузыря после обострения лечится литолитиками: Хенохол, Хенофальк, Эксхол. При отсутствии эффекта проводится ударно-волновая терапия. Пациент продолжает прием ферментов, гепатопротекторов, соблюдение диеты.

В нашем медцентре проводиться устранение любых проявлений данного заболевания. Вы можете пройти консультацию в «Клинике ABC». Для записи вам необходимо воспользоваться телефоном или формой обратной связи на сайте. Администратор подберет наиболее удобное для вас время визита.

Приводим сравнительную таблицу цен на данную процедуру клиник г. Москвы*.

*В соответствии с Федеральным законом о рекламе, мы не указываем название клиник.

1.2 Что такое исчисление и почему мы его изучаем?

Исчисление — это исследование того, как вещи меняются. Он обеспечивает основу для моделирования систем, в которых есть изменение, и способ вывести прогнозы таких моделей.

Я здесь уже какое-то время и знаю, как все в большей или меньшей степени меняется. Что можно добавить к исчислению тот?

Я уверен, вы много знаете о том, как все меняется.И у вас есть качественное представление об исчислении. Например, понятие скорости движения — это понятие прямо из математического анализа, хотя оно, несомненно, существовало задолго до того, как исчисление стало и ты много об этом знаешь.

Так что же мне дает исчисление?

Это дает нам возможность построить относительно простые количественные модели изменений и вывести их последствия.

С какой целью?

Благодаря этому вы получаете возможность обнаруживать влияние изменения условий на исследуемую систему.По изучая их, вы можете узнать, как управлять системой, чтобы заставить ее делать то, что вы хотите. Исчисление, автор предоставление инженерам и вам возможности моделировать и контролировать системы дает им (и потенциально вам) исключительные власть над материальным миром.

Развитие исчисления и его приложений в физике и технике, вероятно, является наиболее значительным фактор в развитии современной науки сверх того, что было во времена Архимеда.И это было ответственны за промышленную революцию и все, что за ней последовало, включая почти все основные достижения последних нескольких веков.

Вы хотите заявить, что я достаточно знаю об исчислении, чтобы моделировать системы и делать выводы, чтобы контролировать их?

Если бы вы задали мне этот вопрос в 1990 году, я бы сказал «нет». Теперь это вполне возможно, поскольку некоторые нетривиальные системы, с использованием вашего ноутбука или настольного компьютера.

Хорошо, но как меняются модели вычислений? Что такое исчисление?

Фундаментальная идея исчисления состоит в том, чтобы изучать изменение путем изучения «мгновенного» изменения, под которым мы понимаем меняется за крошечные промежутки времени.

И что в этом хорошего?

Оказывается, такие изменения, как правило, намного проще, чем изменения за конечные промежутки времени.Это означает их намного легче моделировать. Фактически исчисление было изобретено Ньютоном, который открыл то ускорение, которое означает, что изменение скорости объектов может быть смоделировано его относительно простыми законами движения.

Так вот?

Это оставляет нам проблему получения информации о движении объектов из информации об их скорость или ускорение. А детали исчисления включают взаимосвязь между концепциями, которые иллюстрируются. скоростью и ускорением, а также положением.

Так что же нужно изучать, изучая математику?

Для начала у вас должна быть структура для описания таких понятий, как скорость позиционирования и ускорение.

Исчисление одной переменной, с чего мы начинаем, может иметь дело с движением объекта по фиксированной траектории. В более общая проблема, когда движение может происходить на поверхности или в пространстве, может быть решена многомерным исчисление.Мы изучаем этот последний предмет, находя хитрые уловки для использования одномерных идей и методов. для решения более общих проблем. Таким образом, исчисление одной переменной также является ключом к общей проблеме.

Когда мы имеем дело с объектом, движущимся по пути, его положение меняется со временем, мы можем описать его положение в в любое время одним числом, которое может быть расстоянием в некоторых единицах от некоторой фиксированной точки на этом пути, называемой происхождение нашей системы координат.(Мы добавляем знак к этому расстоянию, которое будет отрицательным, если объект за происхождение.)

Затем движение объекта характеризуется набором его числовых положений в соответствующие моменты времени.

Набор позиций и времени, которые мы используем для описания движения, мы называем функцией . И аналогичные функции используются для описания интересующих величин во всех системах, в которых исчисление применяемый.

Курс здесь начинается с обзора чисел, функций и их свойств. Вы несомненно знакомы с большей частью этого, поэтому мы попытались добавить незнакомый материал, чтобы удержать ваше внимание при просмотре.

Я увязну, если читаю о таких вещах. Должен я?

Я хотел бы, чтобы вы посмотрели на него, так как я это написал, но если вы предпочитаете не делать этого, вы, несомненно, можете обойтись пропуская его и возвращаясь к нему, когда или если вам это нужно.Однако вы пропустите новую информацию, и это может навредить тебе навсегда. (Хотя я в этом сомневаюсь.)

А что после чисел и функций?

Типичный курс математического анализа охватывает следующие темы:

1. Как найти мгновенное изменение (называемое «производной») различных функций. (Процесс выполнения так называется «дифференциация» .)

2.Как использовать производные для решения разного рода проблем.

3. Как вернуться от производной функции к самой функции. (Этот процесс называется «интеграция» .)

4. Изучение детальных методов интегрирования определенных видов функций.

5. Как использовать интеграцию для решения различных геометрических задач, таких как вычисление площадей и объемов определенные регионы.

В этом курсе есть еще несколько стандартных тем. Сюда входит описание функций с точки зрения мощности рядов и изучение того, когда бесконечный ряд «сходится» к числу.

Итак, где это дает мне возможность делать и что?

На самом деле это не так. Проблема в том, что такие курсы были впервые разработаны много веков назад, и они были нацелены на не в расширении прав и возможностей (в то время это было совершенно невозможно), а в ознакомлении аудитории с идеями и концепциями и обозначения, которые позволяют понять более сложную работу.Математики, ученые и инженеры используют концепции исчисления во всевозможных контекстах и используют жаргон и обозначения, которые, без вашего знания о исчисление, было бы совершенно непостижимо для вас. Изучение математического анализа обычно направлено на то, чтобы дать вам «математическая изощренность» применительно к такой более сложной работе.

Так к чему эта чушь о полномочиях?

Этот курс будет стараться отличаться от других и направлен на расширение прав и возможностей, а также на другие обычные цели.Это не может получится, но хотя бы постараюсь.

А как будет пытаться это чудо исполнить?

Традиционные курсы исчисления делают упор на алгебраические методы выполнения дифференцирования и интегрирования. Мы будем описать такие методы, но также показать, как можно выполнять дифференцирование и интеграцию (а также решение обыкновенные дифференциальные уравнения) на компьютерной электронной таблице с приемлемым количеством усилий.Мы также поставлять апплеты, которые делают то же самое автоматически с меньшими усилиями. С помощью этих апплетов или электронной таблицы вы может применять инструменты исчисления с большей легкостью и гибкостью, чем это было возможно раньше.

(Часто доступны более продвинутые программы, такие как MAPLE и Mathematica, которые позволяют делать гораздо больше с такой же легкостью. С их помощью вы можете вывести последствия различных моделей в широком диапазоне. разнообразие контекстов.Как только вы поймете, что такое исчисление, они смогут значительно упростить его использование, но при этом дадут ответы. данные входные данные, что не дает понимания того, как они это делают.)

Также мы будем уделять гораздо больше внимания системам моделирования. С идеями по моделированию и методами решения с помощью дифференциальных уравнений, к которым они приводят, вы можете достичь заявленных нами полномочий.

И я смогу использовать это для какой-нибудь стоящей цели?

Ладно, наверное, нет.Но ты мог бы. А также вас могут спровоцировать узнать больше о системах, которые вы хотите изучать или изучать математику, чтобы улучшить свои шансы на это. Также вы могли бы понять вероятные Последствия моделей немного лучше, чем сейчас. Также вам могут понравиться концепции и идеи исчисление.

Ну, а что во вводной главе о числах?

Начнем с натуральных чисел \ ((1,2,3 ,…) \) и обратите внимание, как операции вычитания, деления и принимая квадратный корень привел нас к расширению нашей системы счисления, включив в нее отрицательные числа, дроби (называемые рациональными числа) и комплексные числа. Мы также описываем десятичные разложения (которые описывают «действительные числа») и исследуем в понятие счетности. Мы тоже бормочем про комплексные числа.

А в главе о функциях?

Мы начинаем с абстрактного определения функции (как набора пар аргумент-значение), а затем описываем стандартные функции.Это те, которые получены, начиная с функции идентичности (значение = аргумент) и экспоненциальная функция и использование различных операций над ними.

Операции, какие операции?

Это сложение, вычитание, умножение, деление, подстановка и инверсия.

Но что такое экспоненциальная функция и что такое подстановка и инверсия?

Вот ответы в одном предложении: если вы хотите узнать больше, прочтите эту главу!

Показательная функция таинственным образом определяется с помощью исчисления: это функция, которая является собственной производной, определено, чтобы иметь значение 1 в аргументе 0.2 \) имеет функцию квадратного корня как обратную.

В бессмертных словах отца Уильяма своему племяннику, написанных математиком Льюисом Кэрроллом:

Я ответил на три вопроса, и этого достаточно,

Сказал мудрец, не надейся.

Как ты думаешь, я могу слушать такие вещи целый день?

Уходи, а то я тебя с лестницы вышвырну!

Что такое исчисление? Определение и практическое применение

Исчисление — это раздел математики, который изучает скорость изменения.До изобретения исчисления вся математика была статичной: она могла помочь вычислить только объекты, которые были совершенно неподвижны. Но вселенная постоянно движется и меняется. Никакие объекты — от звезд в космосе до субатомных частиц или клеток в теле — всегда находятся в состоянии покоя. В самом деле, почти все во Вселенной постоянно движется. Исчисление помогло определить, как частицы, звезды и материя на самом деле движутся и изменяются в реальном времени.

Исчисление используется во множестве областей, в которых, как вы обычно не думали, можно было бы использовать его концепции.Среди них физика, инженерия, экономика, статистика и медицина. Исчисление также используется в таких разрозненных областях, как космические путешествия, а также для определения того, как лекарства взаимодействуют с телом и даже как строить более безопасные структуры. Вы поймете, почему исчисление полезно во многих областях, если вы немного знаете его историю, а также то, для чего он предназначен и для чего он предназначен.

Ключевые выводы: основная теорема исчисления

Исчисление — это исследование скорости изменения.
Готфрид Лейбниц и Исаак Ньютон, математики 17 века, оба независимо изобрели исчисление. Ньютон изобрел ее первым, но Лейбниц создал обозначения, которые математики используют сегодня.
Существует два типа исчисления: дифференциальное исчисление определяет скорость изменения величины, а интегральное исчисление находит величину, скорость изменения которой известна.

Кто изобрел исчисление?

Исчисление было разработано во второй половине 17 века двумя математиками, Готфридом Лейбницем и Исааком Ньютоном.Ньютон первым разработал исчисление и применил его непосредственно к пониманию физических систем. Независимо, Лейбниц разработал обозначения, используемые в исчислении. Проще говоря, в то время как базовая математика использует такие операции, как плюс, минус, время и деление (+, -, x и ÷), в исчислении используются операции, которые используют функции и интегралы для вычисления скорости изменения.

Эти инструменты позволяли Ньютону, Лейбницу и другим математикам вычислять такие вещи, как точный наклон кривой в любой точке.История математики объясняет важность фундаментальной теоремы Ньютона об исчислении:

«В отличие от статической геометрии греков, исчисление позволило математикам и инженерам понять движение и динамические изменения в меняющемся мире вокруг нас, например, орбиты планет, движение жидкостей и т. Д.»

Используя вычисления, ученые, астрономы, физики, математики и химики могли теперь нанести на карту орбиту планет и звезд, а также путь электронов и протонов на атомном уровне.

Дифференциальное и интегральное исчисление

Есть два раздела исчисления: дифференциальное и интегральное. «Дифференциальное исчисление изучает производное и интегральное исчисление … интеграл», — отмечает Массачусетский технологический институт. Но это еще не все. Дифференциальное исчисление определяет скорость изменения количества. Он исследует скорость изменения уклонов и кривых.

Эта ветвь связана с изучением скорости изменения функций по отношению к их переменным, особенно за счет использования производных и дифференциалов.Производная — это наклон линии на графике. Вы найдете наклон линии, рассчитав подъем на пробеге.

Интегральное исчисление, напротив, стремится найти величину, для которой известна скорость изменения. В этом разделе основное внимание уделяется таким понятиям, как наклон касательных линий и скорости. В то время как дифференциальное исчисление сосредотачивается на самой кривой, интегральное исчисление касается пространства или площади под кривой . Интегральное исчисление используется для определения общего размера или значения, например длины, площади и объема.

Исчисление сыграло важную роль в развитии мореплавания в 17 и 18 веках, поскольку позволяло морякам использовать положение Луны для точного определения местного времени. Чтобы определить свое местоположение в море, навигаторам необходимо было уметь точно измерять время и углы. До появления математических методов штурманы и капитаны кораблей не умели ни того, ни другого.

Исчисление — как производное, так и интегральное — помогло улучшить понимание этой важной концепции с точки зрения кривой Земли, расстояния, на которое корабли должны были пройти по кривой, чтобы добраться до определенного места, и даже выравнивания Земли, морей. , и корабли по отношению к звездам.

Практическое применение

Исчисление имеет множество практических приложений в реальной жизни. Некоторые из концепций, использующих исчисление, включают движение, электричество, тепло, свет, гармоники, акустику и астрономию. Исчисление используется в географии, компьютерном зрении (например, для автономного вождения автомобилей), фотографии, искусственном интеллекте, робототехнике, видеоиграх и даже в фильмах. Исчисление также используется для расчета скорости радиоактивного распада в химии и даже для прогнозирования уровней рождаемости и смертности, а также при изучении гравитации и движения планет, потоков жидкости, конструкции кораблей, геометрических кривых и проектирования мостов.

В физике, например, исчисление используется для определения, объяснения и расчета движения, электричества, тепла, света, гармоник, акустики, астрономии и динамики. Теория относительности Эйнштейна основана на исчислении — области математики, которая также помогает экономистам предсказать, какую прибыль может получить компания или отрасль. А в кораблестроении расчет уже много лет используется для определения как кривой корпуса корабля (с помощью дифференциального расчета), так и площади под корпусом (с помощью интегрального расчета), и даже в общей конструкции кораблей. .

Кроме того, исчисление используется для проверки ответов по различным математическим дисциплинам, таким как статистика, аналитическая геометрия и алгебра.

Расчет в экономике

Экономисты используют расчет для прогнозирования спроса, предложения и максимальной потенциальной прибыли. В конце концов, спрос и предложение по существу нанесены на кривую — и притом постоянно меняющуюся кривую.

Экономисты используют расчет для определения эластичности спроса по цене. Они называют постоянно меняющуюся кривую спроса и предложения «эластичной», а действия кривой — «эластичностью».«Чтобы рассчитать точную меру эластичности в определенной точке кривой спроса или предложения, вам нужно подумать о бесконечно малых изменениях цены и, как следствие, включить математические производные в свои формулы эластичности. Расчет позволяет определять конкретные точки на постоянно меняющейся кривой спроса и предложения.

Источник

«Резюме расчетов». Массачусетский технологический институт, 10 января 2000 г., Кембридж, Массачусетс.

Исчисление: основы | Примеры | Что такое Calculus

Исчисление — один из важнейших разделов математики, который имеет дело с постоянными изменениями.Исчисление также называют исчислением бесконечно малых или «исчислением бесконечно малых». Бесконечно малые числа — это величины, значение которых почти равно нулю, но не совсем ноль. Как правило, классическое исчисление — это изучение непрерывной замены функций. Два основных понятия, на которых основано исчисление, — это производные и интегралы.

Производная функции — это мера скорости изменения функции, а интеграл — это мера площади под кривой функции.Производная дает объяснение функции в определенной точке, тогда как интеграл накапливает дискретные значения функции в диапазоне значений.

Введение в исчисление

Calculus фокусируется на некоторых важных математических темах, таких как дифференциация, интеграция, пределы, функции и т. Д. Исчисление, раздел математики, изучающее скорость изменения, был разработан Ньютоном и Лейбницем.

Исчисление Определение: Математическое исчисление обычно используется в математических моделях для получения оптимальных решений и, таким образом, помогает понять различия между значениями, связанными функцией.Исчисление в целом подразделяется на два разных раздела:

Дифференциальное исчисление
Интегральное исчисление

Как дифференциальное, так и интегральное исчисление служат основой для более высокого раздела математики, известного как «Анализ», имеющего дело с влиянием небольшого изменения зависимой переменной, которое приводит к нулю, на функцию.

Темы по исчислению

Ниже приводится список тем, тесно связанных с математическим анализом.Эти темы также дадут вам представление о том, как такие концепции рассматриваются в Cuemath.

Функции

Функции представляют отношения между двумя переменными, которые являются независимой переменной и зависимой переменной. Рассмотрим следующую диаграмму.

Есть ВХОД, черный ящик и ВЫХОД. Например, предположим, что мы хотим приготовить пиццу. Нам понадобятся следующие основные ингредиенты.

Основа для пиццы
Соус для пиццы
Сыр
Приправа

Приведенный выше пример из реальной жизни может быть представлен в форме функции, как объяснено ниже,

Вкус нашей пиццы зависит от качества ингредиентов. Возьмем еще один пример

Предположим, что: y = x ²

Значение x	Значение y
1	1
2	4
9	81
11	121

Используя приведенную выше диаграмму, получаем:

Мы видим, что значение y зависит от значения x.Можно сделать вывод, что

ВХОД не зависит от ВЫХОДА
ВЫХОД зависит от ВХОДА
Черный ящик отвечает за преобразование ВХОДА в ВЫХОД

В расчетах,

INPUT — независимая переменная
ВЫХОД — зависимая переменная
Черный ящик — это функция

Дифференциальное исчисление

Дифференциальное исчисление фокусируется на решении задач определения скорости изменения функции по отношению к другим переменным.Чтобы найти оптимальное решение, производные используются для вычисления максимальных и минимальных значений функции. Дифференциальный помогает в изучении предела частного, имея дело с такими переменными, как x и y, функциями f (x) и соответствующими изменениями переменных x и y. Обозначения dy и dx известны как дифференциалы. Процесс, используемый для нахождения производных, называется дифференцированием. Производная функции y по переменной x представлена как dy / dx или f ’(x).

Пределы

Limit помогает вычислить степень близости к любому значению или приближающемуся члену.Предел обычно выражается с использованием формулы предела как,

lim _{x → c} f (x) = A

Это выражение читается как «предел f для x, когда x приближается к c, равному A».

Производные

Производные представляют собой мгновенную скорость изменения одной величины по отношению к другой. Производная функции представляется как:

lim _{x → h} [f (x + h) — f (x)] / h = A

Непрерывность

Функция f (x) называется непрерывной в определенной точке x = a, если выполняются следующие три условия —

f (a) определено
lim _{x → a} f (x) существует
lim _{x → a ^—} f (x) = lim _{x → a ⁺} f (x) = f (a)

Непрерывность и дифференцируемость

Функция всегда непрерывна, если она дифференцируема в любой точке, тогда как обратное для этого условия не всегда верно.

Интегральное исчисление

Интегральное исчисление — это изучение интегралов и связанных с ними свойств. Это полезно в:

вычисление f по f ’(то есть по его производной). Если функция, скажем, f, дифференцируема в любом заданном интервале, то f ’определена в этом интервале.
вычисление площади под кривой для любой функции.

Интеграция

Интеграция — это обратная связь дифференциации.Поскольку дифференциация может пониматься как разделение части на множество маленьких частей, интеграция может быть названа как совокупность маленьких частей, которые образуют единое целое. Обычно используется для расчета площадей.

Определенный интеграл

Определенный интеграл имеет определенную границу или предел для вычисления функции. Указаны верхний и нижний пределы независимой переменной функции. Математически определенный интеграл задается как,

∫ _a ^b f (x).dx = F (x)

Неопределенный интеграл

Неопределенный интеграл не имеет определенной границы, т. Е. Не определены верхний и нижний предел. Таким образом, значение интегрирования всегда сопровождается постоянным значением (C). Обозначается как:

∫ f (x) .dx = F (x) + C

Приложения исчисления

Исчисление — очень важная отрасль, математическая модель, которая помогает в:

Анализ системы для поиска оптимального решения для предсказания будущего любого заданного состояния функции.
Концепции исчисления играют важную роль в реальной жизни, либо они связаны с решением области сложных форм, оценкой данных опроса, безопасностью транспортных средств, бизнес-планированием, записями о платежах по кредитным картам или обнаружением меняющихся условий системы, влияющих на нас. пр.
Исчисление — это язык экономистов, биологов, архитекторов, медицинских экспертов, статистиков. Например, архитекторы и инженеры используют разные концепции расчета при определении размера и формы строительных конструкций.
Исчисление используется при моделировании таких понятий, как рождаемость и смертность, радиоактивный распад, скорость реакции, тепло и свет, движение, электричество и т. Д.

Часто задаваемые вопросы по исчислению

Что такое исчисление?

Что такое дифференциальное исчисление?

Дифференциальное исчисление фокусируется на решении задач определения скорости изменения функции по отношению к другим переменным. Производная функции y по переменной x представлена как dy / dx или f ’(x).

Для чего вы используете вычисления в реальной жизни?

Концепции исчисления играют важную роль в реальной жизни, либо они связаны с решением области сложных форм, оценкой данных опросов, безопасностью транспортных средств, бизнес-планированием, записями платежей по кредитным картам или поиском изменяющихся условий системы, которая влияют на нас и т. д.Исчисление — это язык экономистов, биологов, архитекторов, медицинских экспертов, статистиков. Например, архитекторы и инженеры используют разные концепции расчета при определении размера и формы строительных конструкций.

Как найти максимумы и минимумы функции?

Чтобы найти оптимальное решение, производные используются для вычисления максимальных и минимальных значений функции. Максимумы и минимумы — это наивысшая и самая низкая точки функции соответственно, которые могут быть определены путем нахождения производной функции.

Что такое интегральное исчисление?

Интегральное исчисление — это изучение интегралов и связанных с ними свойств. Это полезно при вычислении f по f ’(то есть по его производной). Если функция, скажем, f, дифференцируема в любом заданном интервале, то f ’определена в этом интервале. Это позволяет нам рассчитать площадь под кривой для любой функции.

исчисление | Определение и факты

Полная статья

Исчисление , раздел математики, связанный с вычислением мгновенных скоростей изменения (дифференциальное исчисление) и суммированием бесконечно многих малых факторов для определения некоторого целого (интегральное исчисление).Два математика, Исаак Ньютон из Англии и Готфрид Вильгельм Лейбниц из Германии, разделяют заслуги в том, что независимо друг от друга разработали исчисление в 17 веке. Исчисление теперь является основной отправной точкой для всех, кто хочет изучать физику, химию, биологию, экономику, финансы или актуарную науку. Расчет позволяет решать самые разные задачи, например, отслеживание положения космического челнока или прогнозирование давления за плотиной по мере подъема воды. Компьютеры стали ценным инструментом для решения математических задач, которые когда-то считались невероятно сложными.

Расчет кривых и площадей под кривыми

Корни исчисления лежат в некоторых из самых старых известных геометрических проблем. Египетский папирус Ринда ( c. 1650 до н.э.) дает правила определения площади круга и объема усеченной пирамиды. Геометры Древней Греции занимались поиском касательных к кривым, центра тяжести плоских и твердых фигур, а также объемов объектов, образованных вращением различных кривых вокруг фиксированной оси.

Подробнее по этой теме

Анализ
: Исчисление
Не говоря уже о предварительных технических приготовлениях, можно исследовать два фундаментальных аспекта математического анализа:
К 1635 году итальянский математик Бонавентура Кавальери дополнил строгие инструменты греческой геометрии эвристическими методами, которые использовали идею бесконечно малых отрезков линий, площадей и объемов.В 1637 году французский математик-философ Рене Декарт опубликовал свое изобретение аналитической геометрии для алгебраического описания геометрических фигур. Метод Декарта в сочетании с древней идеей кривых, образованных движущейся точкой, позволил математикам, таким как Ньютон, описать движение алгебраически. Внезапно геометры смогли выйти за рамки единичных случаев и специальных методов прежних времен. Они могли видеть закономерности результатов и так предполагать новые результаты, что старый геометрический язык затенял их понимание.
Например, греческий геометр Архимед (287–212 / 211 гг. До н. Э.) Обнаружил изолированным результатом, что площадь сегмента параболы равна определенному треугольнику. Но с алгебраической записью, в которой парабола записывается как y = x ², Кавальери и другие геометры вскоре заметили, что площадь между этой кривой и осью x от 0 до равна . a ³/3 и что аналогичное правило выполняется для кривой y = x ³, а именно, что соответствующая площадь равна a ⁴/4.Отсюда им несложно было догадаться, что общая формула для площади под кривой y = x ⁿ есть a ^{n + 1} / ( n + 1 ).
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Расчет скоростей и уклонов
Проблема нахождения касательных к кривым была тесно связана с важной проблемой, которая возникла в результате исследований движения итальянского ученого Галилео Галилея, а именно с проблемой определения скорости в любой момент частицы, движущейся согласно некоторому закону.Галилей установил, что за t секунд свободно падающее тело падает на расстояние g t ²/2, где g — постоянная (позже интерпретированная Ньютоном как гравитационная постоянная). При определении средней скорости как расстояние за время средняя скорость тела в интервале от t до t + h дается выражением [ g ( t + h ) ²/2 — г т ²/2] / ч .Это упрощается до g t + g h /2 и называется коэффициентом разности функции g t ²/2. Когда h приближается к 0, эта формула приближается к g t , что интерпретируется как мгновенная скорость падающего тела в момент времени t .
Это выражение для движения идентично полученному для наклона касательной к параболе f ( t ) = y = g t ²/2 в точке t .В этом геометрическом контексте выражение g t + g h /2 (или его эквивалент [ f ( t + h ) — f ( t )] / h ) обозначает наклон секущей линии, соединяющей точку ( t , f ( t )) с ближайшей точкой ( t + h , f ( t + h )) ( см. рисунок ). В пределе, с меньшими и меньшими интервалами h , секущая приближается к касательной и ее наклон в точке t .
Таким образом, коэффициент разности можно интерпретировать как мгновенную скорость или как наклон касательной к кривой. Это было исчисление, которое установило эту глубокую связь между геометрией и физикой — в процессе преобразования физики и придания нового импульса изучению геометрии.
Дифференциация и интеграция
Независимо, Ньютон и Лейбниц установили простые правила для нахождения формулы для наклона касательной к кривой в любой точке на ней, имея только формулу для кривой.Скорость изменения функции f (обозначается f ′) называется ее производной. Нахождение формулы производной функции называется дифференцированием, и правила этого составляют основу дифференциального исчисления. В зависимости от контекста производные могут интерпретироваться как наклон касательных линий, скорости движущихся частиц или другие величины, и в этом заключается большая сила дифференциального исчисления.
Важным приложением дифференциального исчисления является построение кривой по ее уравнению y = f ( x ).Это включает, в частности, поиск локальных точек максимума и минимума на графике, а также изменений перегиба (выпуклость на вогнутость или наоборот). При исследовании функции, используемой в математической модели, такие геометрические понятия имеют физические интерпретации, которые позволяют ученому или инженеру быстро получить представление о поведении физической системы.
Другое великое открытие Ньютона и Лейбница заключалось в том, что нахождение производных функций было, в точном смысле, обратной задачей поиска площадей под кривыми — принципа, ныне известного как фундаментальная теорема исчисления.В частности, Ньютон обнаружил, что если существует функция F ( t ), которая обозначает площадь под кривой y = f ( x ), скажем, от 0 до t , то эта функция производная будет равна исходной кривой на этом интервале, F ′ ( t ) = f ( t ). Следовательно, чтобы найти площадь под кривой y = x ² от 0 до t , достаточно найти функцию F так, чтобы F ′ ( t ) = t ².Дифференциальное исчисление показывает, что наиболее общая такая функция — это x ³/3 + C , где C — произвольная константа. Это называется (неопределенным) интегралом функции y = x ² и записывается как ∫ x ² d x . Начальный символ ∫ представляет собой удлиненную букву S, которая обозначает сумму, а d x указывает бесконечно малое приращение переменной или оси, по которой функция суммируется.Лейбниц ввел это, потому что он думал об интегрировании как нахождение площади под кривой путем суммирования площадей бесконечного множества бесконечно малых прямоугольников между осью x и кривой. Ньютон и Лейбниц обнаружили, что интегрирование f ( x ) эквивалентно решению дифференциального уравнения, то есть нахождению функции F ( t ), так что F ′ ( t ) = f ( т ). С физической точки зрения решение этого уравнения можно интерпретировать как нахождение расстояния F ( t ), пройденного объектом, скорость которого имеет заданное выражение f ( t ).
Раздел исчисления, связанный с вычислением интегралов, — это интегральное исчисление, и среди многих его приложений обнаружение работы, выполняемой физическими системами, и вычисление давления за плотиной на заданной глубине.
Джон Л. Берггрен
Узнайте больше в этих связанных статьях Britannica:
Что такое Исчисление
Исчисление — это раздел математики, изучающий пределы, функции, производные, интегралы и бесконечная серия .Этот предмет относится к наиболее важным разделам прикладной математики и служит основой для всей продвинутой математики. расчеты и инженерные приложения.
Категории исчислений
Есть две основные категории математического анализа:

Дифференциальное исчисление
Интегральное исчисление
В этом содержании мы сосредоточимся в основном на различных методах решения исчисления, а также прольем некоторый свет на широкий спектр концепций, связанных с предмет.
Предварительный расчет
Прежде чем мы перейдем к подробному изучению предмета, мы должны быть знакомы с некоторыми основными терминами, связанными с курсом. Хорошее понимание Расчет требует от вас базовых знаний в следующих областях:
Функции
Эти функции далее обозначаются как

Полиномы
Рациональные функции
Логарифмы
Показатели
Тригонометрический
На протяжении всего курса мы будем часто использовать эти термины, поэтому будет лучше, если вы хорошо понимаете термины, перечисленные выше.(n-1) + … + a_1 x + a_0`, где `a_n, a_ (n-1), …, a_0` — действительные числа, а n — неотрицательное целое число. Другими словами, многочлен — это сумма одного или нескольких одночлены с действительными коэффициентами и целыми неотрицательными показателями. Степень полиномиальной функции — это наивысшее значение для n, где n равно не равно 0.
Полиномиальные функции только одного члена называются одночленами или степенными функциями .п`.
Для полиномиальной функции f любое число r, для которого f (r) = 0, называется корнем функции f. Когда полиномиальная функция полностью факторизованный, каждый из факторов помогает определить нули функции.
Рациональные функции
«Рациональная функция» — это имя, данное функции, которая может быть представлена как частное от многочленов, так же как рациональное число является число, которое может быть выражено как частное от целых чисел.Рациональные функции служат важными примерами и естественным образом встречаются во многих контекстах. Все полиномы — рациональные функции.
Логарифмы
Логарифмические функции используются для упрощения сложных вычислений во многих областях, включая статистику, инженерию, химию, физику и музыку. Например, log (xy) = logx + logy и log (x / y) = log x — log y — это логарифмические функции, которые существенно упрощают умножение до сложения и деление до вычитание.Логарифмические функции являются обратными их экспоненциальным аналогам.
Показатели
Экспоненциальная функция — это математическая функция следующего вида: `f (x) = a x` где x — переменная, а a — константа, называемая базой функции. Наиболее часто встречающееся основание экспоненциальной функции — это трансцендентное число e, равное примерно 2.71828. Таким образом, приведенное выше выражение принимает следующий вид: `f (x) = e x` Когда показатель степени в этой функции увеличивается на 1, значение функции увеличивается в e раз. Когда показатель степени уменьшается на 1, значение функции уменьшается на этот же коэффициент (оно делится на e).
Тригонометрический
Функция угла, выраженная как отношение двух сторон прямоугольного треугольника, содержащего этот угол; синус, косинус, тангенс, котангенс, секанс и косеканс.Также называется круговой функцией.
Что такое исчисление 1?
В следующем видео представлен план всех тем, которые вы ожидаете увидеть в типичном классе «Исчисление с одной переменной 1» (например, «Исчисление 1», «Бизнес-исчисление 1», «Исчисление AB», «Исчисление BC или математика IB HL 2») .
Все темы подробно освещены в нашем онлайн-курсе «Исчисление 1».
Онлайн-курс содержит:
Полные лекции — Предназначены для повышения результатов тестов.
150+ HD Video Library — Больше не нужно тратить время на поиски на YouTube.
Доступно 24/7 — Больше никогда не беспокойтесь о том, что пропустите урок.
Практические экзамены — Убедитесь, что вы готовы к выпускным экзаменам.
Математический анализ 1 Syllabus

Исчисление 1 Обзор
В следующих разделах приведены ссылки на наши полные уроки по всем темам «Исчисление 1».
Готовы к исчислению? Узнайте это с помощью нашего БЕСПЛАТНОГО оценочного теста по исчислению.Он включает 22 вопроса, которые помогут вам определить свои сильные и слабые стороны до прохождения курса математического анализа.

Человечеству известно множество разделов математики.Также известный как «язык чисел», он много значит для многих. Некоторые могут знать это как полезный инструмент, который является ключом к получению цивилизаций. прокатка. Но для других они считают это академической досадой, которая только служит к стенограмме более низкого класса. Тем не менее, нельзя отрицать, что математика здесь, чтобы остаться, и на самом деле это часть нашей жизни, вплоть до самые простые вещи.
Одним из важнейших разделов математики является исчисление. Формальное исследование исчисления началось с 17 века известными учеными и математиками как Исаак Ньютон и Готфрид Лейбниц, хотя возможно, что это использовался еще в греческую эпоху.Это математическая дисциплина который в первую очередь касается функций, пределов, производных и интегралов Просто назвать несколько. Эта дисциплина имеет уникальное наследие в истории математики. Несмотря на то, что он разделен между двумя определениями Ньютона и Лейбница, ему все же удалось создать новую математическую систему и использовался во множестве приложений.
Есть 2 различных области исчисления. Первое подполе называется дифференциальное исчисление. Используя концепцию производных функций, он изучает поведение и скорость изменения различных величин.Используя процесс дифференцирования, график функции может быть вычислен, проанализирован, и предсказал. Второе подполе называется интегральным исчислением. Интеграция на самом деле это обратный процесс дифференциации, связанный с концепцией антипроизводной. Либо понятие, либо хотя бы его подобие, существует уже века. Хотя эти 2 подполя обычно отличаются друг от друга, эти две концепции связаны фундаментальными Теорема исчисления.
Хотя исчисление сложно хорошо использовать, у него есть много практических uses — использование, которое вы, вероятно, поначалу не поймете. Самый распространенный практическое использование исчисления при построении графиков определенных формул или функции. Используя такие методы, как первая производная и вторая производная, график и его размеры можно точно оценить. Эти 2 производные используются, чтобы предсказать, как может выглядеть график, в каком направлении в определенной точке, форма графика в определенной точке (если вогнутые или выпуклые), и это лишь некоторые из них.
Когда вы используете исчисление в реальном мире? Фактически, вы можете использовать исчисление разными способами и приложениями. Среди дисциплин, использующих математический анализ включают физику, инженерию, экономику, статистику и медицину. это используется для создания математических моделей, чтобы прийти к оптимальному решению. Например, в физике исчисление используется во многих своих концепциях. Среди физические концепции, использующие концепции исчисления, включают движение, электричество, тепло, свет, гармоники, акустика, астрономия и динамика.На самом деле даже передовые концепции физики, включая электромагнетизм и теорию Эйнштейна теории относительности используют исчисление. В области химии можно использовать исчисление. для прогнозирования таких функций, как скорость реакции и радиоактивный распад. Тем временем, в биологии он используется для определения таких показателей, как рождаемость и смертность. В экономике исчисление используется для вычисления предельных затрат и предельного дохода, позволяя экономистам прогнозировать максимальную прибыль в определенных условиях. В Кроме того, он используется для проверки ответов по разным математическим дисциплинам такие как статистика, аналитическая геометрия и алгебра.
Как видите, исчисление играет огромную роль в реальном мире. Для большинства профессий его изучение — ключ к успеху. Вот почему вы не можете отбросить исчисление как очередная неприятность. Если это так, то интереса к этому вопросу не было бы. длилось столько, сколько было.

калькулезный — это… Что такое калькулезный?

Калькулезный холецистит — симптомы, лечение острого, хронического калькулезного холецистита

Хронический калькулезный холецистит

Острый калькулезный холецистит

Лечение острого калькулезного холецистита

Причины калькулезного простатита и методы лечения

Стоимость услуг по лечению калькулезной формы простатита

что это такое, причины, признаки, симптомы, лечение – МЕДСИ

Оглавление

Классификация

Причины

Холецистит у взрослых — симптомы

Холецистит – признаки заболевания:

Хронический холецистит – симптомы:

Как снять приступ холецистита?

Осложнения

Диагностика

Холецистит – лечение у взрослых

Диета

Преимущества проведения процедуры в МЕДСИ

«Что такое калькулезный холецистит?» – Яндекс.Кью

Хронический калькулезный холецистит

Однопортовая лапароскопическая холецистэктомия SILS

Однопортовая холецистэктомия по методике SILS. Операция при ЖКБ

Симультанная лапароскопическая гистерэктомия и холецистэктомия через единый лапароскопический доступ (S.I.L.S. Port, COVIDIEN)

Симультанная лапароскопическая кардиомиотомия с парциальной фундопликацией в модификации Волковой и холецистэктомия

Лапароскопическая холецистэктомия, диссекция треугольника Кало

Лапароскопическая холецистэктомия при выраженном спаечном процессе (конкремент 5,5 см, объём содержимого 400 мл)

Лапароскопическая холецистэктомия через единый доступ (S.I.L.S. Port COVIDIEN)

Хронический калькулезный холецистит. Лечение от _ руб. в Клинике ABC. Обострение хронического калькулезного холецистита лечение

Анатомическая и генетическая предрасположенность

Профилактика и ключевые симптомы

Как лечить холецистит с ЖКБ?

1.2 Что такое исчисление и почему мы его изучаем?

Что такое исчисление? Определение и практическое применение

Ключевые выводы: основная теорема исчисления

Кто изобрел исчисление?

Дифференциальное и интегральное исчисление

Практическое применение

Расчет в экономике

Источник

Исчисление: основы | Примеры | Что такое Calculus

Введение в исчисление

Темы по исчислению

Функции

Дифференциальное исчисление

Интегральное исчисление

Приложения исчисления

Часто задаваемые вопросы по исчислению

Что такое исчисление?

Что такое дифференциальное исчисление?

Для чего вы используете вычисления в реальной жизни?

Как найти максимумы и минимумы функции?

Что такое интегральное исчисление?

исчисление | Определение и факты

Расчет кривых и площадей под кривыми

Расчет скоростей и уклонов

Дифференциация и интеграция

Узнайте больше в этих связанных статьях Britannica:

Что такое Исчисление

Категории исчислений

Предварительный расчет

Функции

Рациональные функции

Логарифмы

Показатели

Тригонометрический

Что такое исчисление 1?

Математический анализ 1 Syllabus

Получите доступ ко всем курсам и более 150 HD-видео с подпиской

Еще не готовы подписаться? Испытайте Calcworkshop на нашем БЕСПЛАТНОМ курсе с ограничениями

Что такое исчисление? Когда вы используете это в реальном мире?

Что такое исчисление? Когда вы используете это в реальном мире?

Веб-сайты для изучения исчислений

Добавить комментарий Отменить ответ